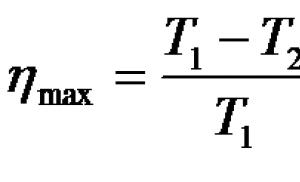Магнитная энергия контура с током. Энергия магнитного поля

Энергия магнитного поля при наличии магнетиков

Пусть все рассматриваемое пространство заполняет однородный магнетик. В нем индукция магнитного поля, которое создают токи, изменяется в $\mu $ раз в сравнении с индукцией в вакууме. Во столько же изменяются магнитные потоки $Ф$ и $dФ.$ Элементарная работа, выполняемая внешним источником против электродвижущей силы индукции, будет равна:

Допустим, что магнитное поле создается двумя контурами. Если $L_{11}$ - индуктивность первого контура, $L_{22}$ - индуктивность второго контура, то можно записать, что:

Поток ${\Phi }_{12}$, который пересекает контур (1), создаваемый током во втором контуре равен:

где $L_{12}$- постоянная, взаимная индуктивность первого и второго контуров. Для второго контура имеем:

Из формул (2) - (4) следует, что если изменяются магнитные потоки в магнетике, то индукции контура и взаимные индукции увеличиваются в $\mu $ раз. Это значит, что взаимные индукции контуров равны:

При этом магнитные потоки в магнитике могут быть выражены как:

где $r_{21}=r_{12}$ - расстояния между элементами контуров с током $d\overrightarrow{l_1}и\ d\overrightarrow{l_2}$.

Формула же записанная для энергии магнитного поля , которое создано двумя контурами с токами для вакуума и магнетика (при отсутствии ферромагнетика) по форме не изменяется:

Если магнитное поле образуется $N$ контурами, то его энергию можно вычислить как:

Рисунок 1.

при $i=k$ коэффициент $L_{ik}$ называется индуктивностью контура ${\rm I}$, при $i\ne k$, этот же коэффициент называют взаимной индуктивностью ${\rm I}$-го и k-го контуров. Эти коэффициенты определяются формулами при $i\ne k$:

где $d\overrightarrow{l_i},d\overrightarrow{l_k}$ - элементы длины контуров ${\rm I}$-го и $k$-го. $r_{ik}-$расстояние между ними. При этом $L_{ik}=L_{ki}$. В результате получается, что энергия магнитного поля токов, которые текут в неограниченном однородном магнетике, изменяется в $\mu $ раз в сравнении с энергией этих же токов в вакууме.

Объемная плотность энергии магнитного поля

Магнитное поле, которое создают токи, распределено по всему пространству. Допустим, что магнитное поле создается одиночным контуром с током. Магнитная энергия поля в таком случае может быть представлена как:

где поток магнитной индукции можно выразить как:

где $L$ контур тока, $S$ - поверхность, которая натянута на контур $L$, $\overrightarrow{A}\ $- векторный потенциал, магнитного поля, которое создается током $I$. Замкнутый ток взаимодействует со своим магнитным полем. Каждый элемент тока $Id\overrightarrow{l}$ создает в пространстве собственное магнитное поле, с которым взаимодействуют другие элементы тока.

Подставим (11) в формулу (10), получим:

Проведем переход от линейных токов к объемным токам с помощью соотношения:

Из выражения (10) получим:

Используем известные формулы:

Преобразуем выражение (12), получим:

По теореме Остроградского - Гаусса имеем:

В том случае, если точки рассматриваются в конечной области пространства, на больших расстояниях от этой области $A\sim \frac{1}{r}$, $H\sim \frac{1}{r^2}$, то есть подынтегральное выражение убывает пропорционально $\frac{1}{r^3}$. Поверхность при этом растет пропорционально $r^2$, получаем, что интеграл уменьшается $\sim \frac{1}{r}.$ Получается, что при $r\to \infty $, второй интеграл в выражении (15) равен нулю, тогда полная энергия выражается формулой:

Тогда, можно сказать, что объемная плотность энергии магнитного поля в пространстве равна:

Энергия магнетика во внешнем поле

Если имеется фиксированное распределение токов в пространстве, то энергия магнетика в магнитном поле равна:

где $\overrightarrow{J}$ - намагниченность магнетика, $\overrightarrow{B_0}$ - магнитное поле в свободном пространстве.

Пример 1

Задание: Вычислите магнитную проницаемость железа, если в поле с индукцией $B=1Тл$ плотность энергии магнитного поля в веществе $200 \frac{Дж}{м^3}$.

Решение:

Из формулы (1.1) выразим магнитную проницаемость, получим:

\[\mu =\frac{1}{2}\frac{B^2}{w_m{\mu }_0}\left(1.2\right).\]

Проведем вычисления:

\[\mu =\frac{1}{2}\cdot \frac{1^2}{200\cdot 1,26\cdot {10}^{-6}}=2\cdot {10}^3.\]

Ответ: $\mu =2\cdot {10}^3.$

Пример 2

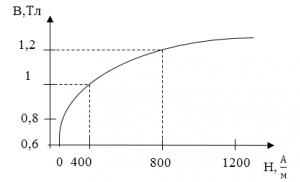
Задание: Определите, как изменится объемная плотность энергии магнитного поля, если индукция магнитного поля тороида, который имеет ферромагнитный сердечник, увеличилась от $B_1=0,9\ Тл\ до\ B_2=1,2\ Тл$. Зависимость $B(H)$ представлена графиком на рис.2.

Рисунок 2.

Решение:

В качестве основания для решения задачи используем формулу

Запишем формулу (2.1) для двух состояний магнитного поля и найдем отношение $\frac{w_{2m}}{w_{1m}}$:

\[\frac{w_{2m}}{w_{1m}}=\frac{1}{2}H_2B_2\cdot 2\frac{1}{H_1B_1}=\frac{H_2B_2}{H_1B_1}\left(2.2\right).\]

По графику находим, что при $B_1=1\ Тл\ H_1=400\frac{A}{м}\ до\ B_2=1,2\ Тл\ H_2=800\frac{A}{м}\ $.

Следовательно, искомое отношение равно:

\[\frac{w_{2m}}{w_{1m}}=\frac{1,2\cdot 800}{1\cdot 400}=2,4.\]

Ответ: $\frac{w_{2m}}{w_{1m}}=2,4.\ $

Если в контуре с индуктивностью L течёт ток I, то в момент размыкания цепи возникает индукционный ток и им совершается работа. Эта работа совершается за счёт энергии исчезнувшего при размыкании цепи магнитного поля. На основании закона сохранения и превращения энергию магнитного поля превращается главным образом в энергию электрического поля, за счёт которой происходит нагревание проводников. Работа может быть определена из соотношения

Так как , то

Уменьшение энергии магнитного поля равно работе тока, поэтому

(16.18)

Формула справедлива для любого контура и показывает, что энергия магнитного поля зависит от индуктивности контура и силы тока, протекающего по нему.

Рассчитаем энергию однородного магнитного поля длинного соленоида, индуктивность которого определяется по формуле L = μμ 0 n 2 V. B этом случае формула энергии примет вид

Учитывая, что напряжённость поля внутри бесконечно длинного соленоида Н=In, получаем

(16.19)

Выразим энергию через индукцию магнитного поля B= μμ 0 H:

(16.20)

(16.21)

Вследствие того, что магнитное поле соленоида однородно и локализовано внутри соленоида, энергия распределена по объёму соленоида с постоянной плотностью

(16.22)

Учитывая последние три формулы, получаем

Учитывая правило Ленца, можно заметить, что явление самоиндукции аналогично проявлению инертности тел в механике. Так, вследствие инертности тело не мгновенно приобретает определённую скорость, а постепенно. Так же постепенно происходит и его торможение. То же самое, как мы видели, происходит и с силой тока при самоиндукции. Эту аналогию можно провести и дальше.

и

эти уравнения эквивалентны.

т.е. m ~L , υ~I

Эквивалентны и формулы

Примеры решения задач

Пример . В магнитном поле, изменяющемся по закону B=B 0 cosωt (B 0 =5мТл,

ω=5с -1), помещён круговой проволочный виток радиусом r=30см, причём нормаль к витку образует с направлением поля угол α=30º. Определите ЭДС индукции, возникающую в витке в момент времени t=10с.

Дано : B=B 0 cosωt; B 0 =5мТл=5∙10 -3 Тл; ω=5с -1 ; r=30см=0,3 м; α=30º; t=10 с.

Найти: ε i .

Решение: Согласно закону Фарадея,

, (1)

Где магнитный поток, сцепленный с витком при произвольном его расположении относительно магнитного поля.

По условию задачи B=B 0 cosωt, а площадь кольца S=πr 2 , поэтому

Ф=πr 2 B 0 cosωt∙cosα. (2)

Подставив выражение (2) в формулу (1) и продифференцировав, получаем искомую ЭДС индукции в заданный момент времени:

Ответ: ε i =4,69 мВ.

Пример В соленоиде длиной ℓ=50см и диаметром d=6см сила тока равномерно увеличивается на 0,3А за одну секунду. Определите число витков соленоида, если сила индукционного тока в кольце радиусом 3,1 см из медной проволоки (ρ=17нОм∙м), надетом на катушку, I к =0,3 А.

Дано: ℓ=50см=0,5 м; d=6см=0,06м;
;r к =3,1см=3.1∙10 -2 м; ρ=17нОм∙м=17∙10 -9 Ом∙м; I к =0,3 А.

Найти : N.

Решение . При изменении силы тока в соленоиде возникает ЭДС самоиндукции

(1)

где
- индуктивность соленоида. Подставив это выражение в (1)

с учётом

.

ЭДС индукции, возникающая в одном кольце, в N раз меньше, чем найденное значение ЭДС самоиндукции в соленоиде, состоящем из N витков, т.е.

. (2)

Согласно закону Ома, сила индукционного тока в кольце

, (3)

где
- сопротивление кольца. Поскольку ℓ к =πd, а S к =πr к 2 , выражение (3) примет вид

Подставив в эту формулу выражение (2), найдём искомое число витков соленоид

.

Ответ : N=150

Пример В однородном магнитном поле подвижная сторона (её длина ℓ=20см) прямоугольной рамки (см. рисунок) перемещается перпендикулярно линиям магнитной индукции со скоростью υ=5 м/с. Определите индукцию В магнитного поля, если возникающая в рамке ЭДС индукции ε i =0,2 В.

Дано: ℓ=20см=0,2 м; υ=5 м/с; ε i =0,2 В.

Найти : B.

Р
ешение . При движении в магнитном поле подвижной стороны рамки поток Ф вектора магнитной индукции сквозь рамку возрастает, что, согласно закону Фарадея,

, (1)

приводит к возникновению ЭДС индукции.

Поток вектора магнитной индукции, сцепленный с рамкой,

Подставив выражение (2) в формулу (1) и учитывая, что B и ℓ - величины постоянные, получаем

откуда искомая индукция магнитного поля

Ответ : В=0,2 Тл.

Пример В однородном магнитном поле с индукцией В=0,2 Тл равномерно вращается катушка, содержащая N=600 витков, с частотой n=6 с -1 . Площадь S поперечного сечения катушка 100см 2 . Ось вращения перпендикулярна оси катушки и направлению магнитного поля. Определите максимальную ЭДС индукции вращающейся катушки.

Дано: В=0,2 Тл; N=600; n=6 с -1 ; S=100см 2 =10 -2 м 2 .

Найти : (ε i) max .

Решение . Согласно закону Фарадея,

где Ф – полный магнитный поток, сцеплённый со всеми витками катушки. При произвольном расположении катушки относительно магнитного поля

Ф=NBScosωt, (1)

где круговая частота ω=2πn. Подставив ω в (1), получим

ε i =-NBS2πn(-sin2πnt)=2πnNBSsin2πnt,

ε i =(ε i) max при sin2πnt=1, поэтому

(ε i) max =2πnNBS

Ответ : (ε i) max =45,2 В.

Пример Однослойная длинная катушка содержит N=300 витков, плотно прилегающих друг к другу. Определите индуктивность катушки, если диаметр проволоки d=0,7 мм (изоляция ничтожной толщины) и она намотана на картонный цилиндр радиусом r=1 см. .

Дано: N=300; d=0,7 мм=7∙10 -4 м; r=1 см=10 -2 м.

Найти : L.

Решение . Индуктивность катушки

(1)

где Ф – полный магнитный поток, сцепленный со всеми витками катушки; I - сила тока в катушке.

Учитывая, что полный магнитный поток

(N-число витков катушки; В – магнитная индукция; S – площадь поперечного сечения катушки); магнитная индукция в катушке без сердечника

(μ 0 – магнитная постоянная; ℓ- длина катушки), длина катушки

(d-диаметр проволоки; витки вплотную прилегают друг к другу), площадь поперечного сечения катушки

Получим осле подстановки записанных выражений в формулу (1) искомую индуктивность катушки:

Ответ: L=1,69 мГн.

Пример Первичная обмотка понижающего трансформатора с коэффициентом трансформации k=0,1 включена в сеть с источником переменного напряжения с ЭДС ε 1 =220 В. Пренебрегая потерями энергии в первичной обмотке, определите напряжение U 2 на зажимах вторичной обмотки, если её сопротивление R 2 =5 Ом и сила тока в ней I 2 =2А.

Дано: k=0,1; ε 1 =220 В; R 2 =5 Ом; I 2 =2А.

Найти : U 2 .

Решение . В первичной обмотке под действием переменной ЭДС ε 1 возникает переменный ток I 1 , создающий в сердечнике трансформатора переменногый магнитный поток Ф, который пронизывает вторичную обмотку. Согласно закону Ома, для первичной обмотки

где R 1 – сопротивление первичной обмотки. Падение напряжения I 1 R 1 при быстропеременных полях мало по сравнению с ε 1 и ε 2 . Тогда можем записать:

(1)

ЭДС взаимной индукции, возникающая во вторичной обмотке,

(2)

Из выражений (1) и (2) получаем

,

где
- коэффициент трансформации, а знак «-» показывает, что ЭДС в первичной и вторичной обмотках противоположны по фазе. Следовательно, ЭДС во вторичной обмотке

Напряжение на зажимах вторичной обмотки

U 2 = ε 2 -I 2 R 2 = kε 1 -I 2 R 2 .

Ответ : U 2 =12 В.

Пример Соленоид без сердечника с однослойной обмоткой из проволоки диаметром d=0,4 мм имеет длину ℓ=0.5 м и поперечное сечение S=60см 2 . За какое время при напряжении U=10 В и силе тока I=1,5 А в обмотке выделится количество теплоты, равное энергии поля внутри соленоида? Поле считать однородным.

Дано: d=0,4 мм=0,4∙10 -4 м; ℓ=0,5 м; S=60см 2 =6∙10 -3 м 2 ; I=1,5А; U=10В; Q=W.

Найти : t.

Решение . При прохождении тока I при напряжении U в обмотке за время t выделяется теплота

Энергия поля внутри соленоида

(2)

где
(N – общее число витков соленоида). Если витки вплотную прилегают друг к другу, то ℓ=Nd, откуда
. Подставив выражение для В иN в (2), получаем

. (3)

Согласно условию задачи, Q=W. Приравняв выражение (1) и (3),найдём искомое время:

Ответ: t =1,77 мс.

Пример Катушка без сердечника длиной ℓ=50 см содержит N=200 витков. По катушке течёт ток I=1А. Определите объёмную плотность энергии магнитного поля внутри катушки..

Дано : ℓ=50 см=0,5 м; N=200; I=1 А.

Найти : ω.

Решение . Объёмная плотность энергии магнитного поля (энергия единицы объёма)

, (1)

где
- энергия магнитного поля (L - индуктивность катушки); V=Sℓ- объём катушки (S - площадь катушки; ℓ- длина катушки).

Магнитная индукция поля внутри соленоида с сердечником с магнитной проницаемостью μ равна

.

Полный магнитный поток, сцепленный со всеми витками соленоида,

.

Учитывая, что Ф=LI, получаем формулу для индуктивности соленоида:

(2)

Подставив выражение (2) в формулу (1) с учётом того, что
, найдём искомую объёмную плотность энергии магнитного поля внутри катушки:

B {\displaystyle \mathbf {B} } (вектор индукции магнитного поля) . С математической точки зрения B = B (x , y , z) {\displaystyle \mathbf {B} =\mathbf {B} (x,y,z)} - векторное поле , определяющее и конкретизирующее физическое понятие магнитного поля.

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал .

Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие магнитной среды) выбирают не вектор магнитной индукции B , {\displaystyle \mathbf {B} ,} а вектор напряжённости магнитного поля , что формально можно сделать, так как в вакууме эти два вектора совпадают ; однако в магнитной среде вектор H {\displaystyle \mathbf {H} } не несёт уже того же физического смысла , являясь важной, но всё же вспомогательной величиной. Поэтому при формальной эквивалентности обоих подходов для вакуума, с систематической точки зрения следует считать основной характеристикой магнитного поля именно B . {\displaystyle \mathbf {B} .}

Магнитное поле можно назвать особым видом материи , посредством которой осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом .

Магнитные поля являются необходимым (в контексте специальной теории относительности) следствием существования электрических полей.

• С точки зрения квантовой теории поля магнитное взаимодействие - как частный случай электромагнитного взаимодействия переносится фундаментальным безмассовым бозоном - фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля), часто (например, во всех случаях статических полей) - виртуальным.

Источники магнитного поля

Магнитное поле создаётся (порождается) током заряженных частиц , или изменяющимся во времени электрическим полем , или собственными магнитными моментами частиц (последние для единообразия картины могут быть формальным образом сведены к электрическим токам).

Вычисление

В простых случаях магнитное поле проводника с током (в том числе и для случая тока, распределённого произвольным образом по объёму или пространству) может быть найдено из закона Био - Савара - Лапласа или теоремы о циркуляции (она же - закон Ампера). Этот способ ограничивается случаем (приближением) магнитостатики - то есть случаем постоянных (если речь идёт о строгой применимости) или достаточно медленно меняющихся (если речь идёт о приближенном применении) магнитных и электрических полей.

В более сложных ситуациях ищется как решение уравнений Максвелла .

Проявление магнитного поля

Магнитное поле проявляется в воздействии на магнитные моменты частиц и тел, на движущиеся заряженные частицы (или проводники с током). Сила, действующая на движущуюся в магнитном поле электрически заряженную частицу, называется силой Лоренца , которая всегда направлена перпендикулярно к векторам v и B . Она пропорциональна заряду частицы q , составляющей скорости v , перпендикулярной направлению вектора магнитного поля B , и величине индукции магнитного поля B . В Международной системе единиц (СИ) сила Лоренца выражается так:

F = q [ v , B ] , {\displaystyle \mathbf {F} =q[\mathbf {v} ,\mathbf {B} ],} F = q c [ v , B ] , {\displaystyle \mathbf {F} ={\frac {q}{c}}[\mathbf {v} ,\mathbf {B} ],}

где квадратными скобками обозначено векторное произведение .

Также (вследствие действия силы Лоренца на движущиеся по проводнику заряженные частицы) магнитное поле действует на проводник с током . Сила, действующая на проводник с током называется силой Ампера . Эта сила складывается из сил, действующих на отдельные движущиеся внутри проводника заряды.

Взаимодействие двух магнитов

Одно из наиболее часто встречающихся в обычной жизни проявлений магнитного поля - взаимодействие двух магнитов : одинаковые полюса отталкиваются, противоположные притягиваются. Представляется заманчивым описать взаимодействие между магнитами как взаимодействие между двумя монополями , и с формальной точки зрения эта идея вполне реализуема и часто весьма удобна, а значит практически полезна (в расчётах); однако детальный анализ показывает, что на самом деле это не полностью правильное описание явления (наиболее очевидным вопросом, не получающим объяснения в рамках такой модели, является вопрос о том, почему монополи никогда не могут быть разделены, то есть почему эксперимент показывает, что никакое изолированное тело на самом деле не обладает магнитным зарядом; кроме того, слабостью модели является то, что она неприменима к магнитному полю, создаваемому макроскопическим током, а значит, если не рассматривать её как чисто формальный приём, приводит лишь к усложнению теории в фундаментальном смысле).

Правильнее будет сказать, что на магнитный диполь , помещённый в неоднородное поле, действует сила, которая стремится повернуть его так, чтобы магнитный момент диполя был сонаправлен с магнитным полем. Но никакой магнит не испытывает действия (суммарной) силы со стороны однородного магнитного поля. Сила, действующая на магнитный диполь с магнитным моментом m выражается по формуле :

F = (m ⋅ ∇) B . {\displaystyle \mathbf {F} =\left(\mathbf {m} \cdot \nabla \right)\mathbf {B} .}

Сила, действующая на магнит (не являющийся одиночным точечным диполем) со стороны неоднородного магнитного поля, может быть определена суммированием всех сил (определяемых данной формулой), действующих на элементарные диполи, составляющие магнит.

Впрочем, возможен подход, сводящий взаимодействие магнитов к силе Ампера, а сама формула выше для силы, действующей на магнитный диполь, тоже может быть получена, исходя из силы Ампера.

Явление электромагнитной индукции

История развития представлений о магнитном поле

Хотя магниты и магнетизм были известны гораздо раньше, изучение магнитного поля началось в 1269 году, когда французский учёный Пётр Перегрин (рыцарь Пьер из Мерикура) отметил магнитное поле на поверхности сферического магнита, применяя стальные иглы, и определил, что получающиеся линии магнитного поля пересекались в двух точках, которые он назвал «полюсами » по аналогии с полюсами Земли. Почти три столетия спустя, Уильям Гильберт Колчестер использовал труд Петра Перегрина и впервые определённо заявил, что сама Земля является магнитом. Опубликованная в 1600 году, работа Гилберта «De Magnete » , заложила основы магнетизма как науки.

Три открытия подряд бросили вызов этой «основе магнетизма». Во-первых, в 1819 году Ханс Кристиан Эрстед обнаружил, что электрический ток создаёт магнитное поле вокруг себя. Затем, в 1820 году, Андре-Мари Ампер показал, что параллельные провода, по которым идёт ток в одном и том же направлении, притягиваются друг к другу. Наконец, Жан-Батист Био и Феликс Савар в 1820 году открыли закон, названный законом Био-Савара-Лапласа , который правильно предсказывал магнитное поле вокруг любого провода, находящегося под напряжением.

Расширив эти эксперименты, Ампер издал свою собственную успешную модель магнетизма в 1825 году. В ней он показал эквивалентность электрического тока в магнитах, и вместо диполей магнитных зарядов модели Пуассона, предложил идею, что магнетизм связан с постоянно текущими петлями тока. Эта идея объясняла, почему магнитный заряд не может быть изолирован. Кроме того, Ампер вывел закон, названный его именем , который, как и закон Био-Савара-Лапласа, правильно описал магнитное поле, создаваемое постоянным током, а также была введена теорема о циркуляции магнитного поля . Кроме того, в этой работе, Ампер ввёл термин «электродинамика » для описания взаимосвязи между электричеством и магнетизмом.

Между 1861 и 1865 годами Джеймс Клерк Максвелл разработал и опубликовал уравнения Максвелла , которые объяснили и объединили электричество и магнетизм в классической физике . Первая подборка этих уравнений была опубликована в статье в 1861 году, озаглавленной «On Physical Lines of Force » . Эти уравнения были признаны действительными, хотя и неполными. Максвелл завершил свои уравнения в своей более поздней работе 1865 года

Согласно азам физики, известно о наличии магнитного поля вокруг проводника или катушки с током. Данное поле в полной мере зависит от проводника, среды распространения поля и силы тока. Аналогично электрическому полю, магнитное поле является неким носителем энергии. Поскольку основным критерием, влияющим на энергию поля, является сила протекающего тока, то работа тока по созданию магнитного поля будет совпадать с энергией магнитного поля.

Энергия магнитного поля

Природу такого явления, как энергия магнитного поля, проще осознать, рассмотрев процессы, проходящие в цепи.

Элементы схемы:

1. L – катушка индуктивности;
2. Л – лампочка;
3. ε – источник постоянного тока;
4. К – ключ для замыкания и размыкания цепи.

При замкнутом ключе, согласно картинке (а), ток протекает от плюсовой клеммы источника тока по параллельным веткам через катушку индуктивности и лампочку. По катушке индуктивности протекает ток I0, а через лампочку протекает ток I1. В первый момент времени лампочка будет гореть более ярко, ввиду большого сопротивления катушки индуктивности. По мере уменьшения сопротивления катушки индуктивности и увеличения тока I0 лампочка будет гореть более тускло. Это объясняется тем, что в первый момент времени поступивший на катушку ток пропорционален току большой частоты, исходя из формулы индуктивного сопротивления катушки:

XL=2πfL, где:

• XL – индуктивное сопротивление катушки;
• f – частота тока;
• L – индуктивность катушки.

Индуктивное сопротивление катушки возрастает многократно. Катушка индуктивности в этот момент времени ведет себя как разрыв цепи. Со временем индуктивное сопротивление снижается до нуля. Поскольку активное сопротивление катушки индуктивности ничтожно мало, а сопротивление нихромовой нити лампочки велико, то практически весь ток цепи протекает через катушку.

После размыкания цепи ключом К, согласно картинке (б), лампочка не тухнет, а, наоборот, загорается более ярким светом и постепенно гаснет. Для осуществления горения лампочки необходима энергия. Энергия эта берется из магнитного поля катушки индуктивности и называется энергией магнитного поля. Благодаря этому катушка индуктивности выступает как источник энергии (самоиндукции), согласно картинке (в).

Определить активность магнитного поля возможно, рассмотрев электрическую схему.

Для расчета энергии магнитного поля есть необходимость в создании такой схемы, в которой энергия источника питания расходовалась бы непосредственно на образование магнитного поля. Соответственно, в схеме выше значениями внутреннего сопротивления источника питания и катушки индуктивности нужно пренебречь.

Обратите внимание! Из второго закона Кирхгофа следует, что сумма напряжений, подключенных к цепи, равна сумме падений напряжений на каждом из элементов цепи.

Общее напряжение цепи равно:

ε+εі=Ir+IR, где:

• ε – электродвижущая сила (напряжение) источника питания;
• εi – электродвижущая сила (напряжение) индукции;
• I – сила тока цепи;
• r – внутреннее сопротивление источника питания;
• R – внутреннее сопротивление катушки индуктивности.

Поскольку рассмотренная цепь идеальная, и внутренние сопротивления равны нулю, то формула преобразовывается в такую:

Электродвижущая сила самоиндукции зависит от индуктивности катушки и скорости изменения тока в цепи, а именно:

подставив значение в общую формулу, получается:

• ε-LΔI/Δt=0,
• ε= LΔI/Δt,
• ΔI= ε Δt /L.

Исходя из данной закономерности, с течением времени сила тока равняется:

Заряд, пройденный через катушку индуктивности, равен:

Объединив обе формулы, получаем:

Работа источника тока по переносу заряда по катушке индуктивности равняется:

A= εq=εLI2/2ε=LI2/2.

Поскольку рассматриваемая цепь является идеальной, а именно отсутствует какое-либо сопротивление, то затраченная работа источника тока пошла на формирование магнитного поля и соответствует энергии магнитного поля:

С целью исключения зависимости активности магнитного поля от характеристики катушки, необходимо преобразовать выражение через характеристику поля, а именно через вектор магнитной индукции:

1. B=µ0µIn, где:

• B – вектор магнитной индукции соленоида;
• µ0 – магнитная постоянная (µ0=4π×10-7 Гн/м)
• µ – магнитная проницаемость вещества;
• I – сила тока в цепи соленоида;
• n – плотность намотки, (n=N/l, где N – число витков, l – отрезок длины соленоида).

1. L=µ0µn2V, где:

V – объем катушки (или объем магнитного поля, сосредоточенного в катушке) (V=Sl, S – площадь поперечного сечения соленоида, l – длина соленоида).

Если воспользоваться формулами (1 и 2), выражение, определяющее энергию магнитного поля, выглядит как:

Wмаг=B2V/2µ0µ.

Рассмотренная формула справедлива при условии, что фон однотипный. Если поле неоднородное, то необходимо рассматривать параметр, характеризующий концентрацию активности в этой зоне. Эта величина именуется как объемная плотность энергии магнитного поля.

Объемная плотность магнитной энергии

Она определяется по выражению:

ωмаг=Wмаг/V, где:

• ωмаг – объемная плотность энергии магнитного поля;
• V – объем некой зоны, где создано магнитное поле.

Единицей измерения объемной плотности энергии магнитного поля является отношение – Дж/м3.

Подставив в искомое выражение значение энергии поля W маг, получаем окончательную формулировку, определяющую объемную плотность:

ωмаг= B2/2µ0µ.

Изложенная информация подробно раскрывает порядок нахождения такого параметра поля, как энергия магнитного поля. Поскольку указанная величина применима для однородного поля, то для проведения вычислений в неоднородном магнитном поле используется величина, определяющая концентрацию или плотность энергии поля.

Видео

Энергия магнитного поля.

Магни́тное по́ле - силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения, магнитная составляющая электромагнитного поля

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).

Энергия магнитного поля , создаваемого током в замкнутом контуре индуктивностью L, равна где I - сила тока в контуре.

Энергия магнитного поля катушки с индуктивностью L, создаваемого током I, равна

Энергия магнитного поля

Проводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока. Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля.

L, по которому течет ток I . С данным контуром сцеплен магнитный поток (см. (126.1)) Ф=LI, I L dI А=I dФ=LI dI.

Так как I=Bl/ (m 0 mN ) (см. (119.2)) и В=m 0 mH (см. (109.3)), то

(130.2)

где Sl = V - объем соленоида.

(130.3)

В от Н линейная, т.е. оно относится только к пара- и диамагнетикам.

Энергия электромагнитного поля

Эне́ргия электромагни́тного по́ля - энергия, заключенная в электромагнитном поле[источник не указан 1754 дня ]. Сюда же относятся частные случаи чистого электрического и чистого магнитного поля.

Работа электрического поля по перемещению заряда

Понятие работы A {\displaystyle A} электрического поля E {\displaystyle E} по перемещению заряда Q {\displaystyle Q} вводится в полном соответствии с определением механической работы:

A = ∫ F (x) d x = ∫ Q ⋅ E (x) d x = Q ⋅ U {\displaystyle A=\int F(x)\,dx=\int Q\cdot E(x)\,dx=Q\cdot U}

где U = ∫ E d x {\displaystyle U=\int E\,dx} - разность потенциалов (также употребляется термин напряжение).

Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов U (t) {\displaystyle U(t)} , в таком случае формулу для работы следует переписать следующим образом:

A = ∫ U (t) d Q = ∫ U (t) I (t) d t {\displaystyle A=\int U(t)\,dQ=\int U(t)I(t)\,dt}

где I (t) = d Q d t {\displaystyle I(t)={dQ \over dt}} - сила тока.

Мощность электрического тока в цепи

Мощность W {\displaystyle W} электрического тока для участка цепи определяется обычным образом, как производная от работы A {\displaystyle A} по времени, то есть выражением:

W (t) = d A d t = U (t) ⋅ I (t) {\displaystyle W(t)={\frac {dA}{dt}}=U(t)\cdot I(t)}

Это наиболее общее выражение для мощности в электрической цепи.

С учётом закона Ома

U = I ⋅ R {\displaystyle U=I\cdot R}

электрическую мощность, выделяемую на сопротивлении R {\displaystyle R} , можно выразить как через ток

W = I (t) 2 ⋅ R {\displaystyle W=I(t)^{2}\cdot R} ,

так и через напряжение:

W = U (t) 2 R {\displaystyle W={{U(t)^{2}} \over R}}

Соответственно, работа (выделившаяся теплота) является интегралом мощности по времени:

A = ∫ W (t) d t = ∫ I (t) 2 ⋅ R d t = ∫ U (t) 2 R d t {\displaystyle A=\int W(t)\,dt=\int I(t)^{2}\cdot R\,dt=\int {{U(t)^{2}} \over R}\,dt}

Энергия электрического и магнитного полей

Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Строго говоря, термин «энергия электромагнитного поля» является не вполне корректным. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определённой точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.

Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.

В системе СИ:

U = E ⋅ D 2 + B ⋅ H 2 {\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}}

В вакууме (а также в веществе при рассмотрении микрополей):

U = ε 0 E 2 2 + B 2 2 μ 0 = ε 0 E 2 + c 2 B 2 2 = E 2 / c 2 + B 2 2 μ 0 {\displaystyle u={\varepsilon _{0}E^{2} \over 2}+{B^{2} \over {2\mu _{0}}}=\varepsilon _{0}{\frac {E^{2}+c^{2}B^{2}}{2}}={\frac {E^{2}/c^{2}+B^{2}}{2\mu _{0}}}}

где E - напряжённость электрического поля, B - магнитная индукция, D - электрическая индукция, H - напряжённость магнитного поля, с - скорость света, ε 0 {\displaystyle \varepsilon _{0}} - электрическая постоянная и μ 0 {\displaystyle \mu _{0}} - магнитная постоянная. Иногда для констант ε 0 {\displaystyle \varepsilon _{0}} и μ 0 {\displaystyle \mu _{0}} - используют термины диэлектрическая проницаемость и магнитная проницаемость вакуума, - которые являются крайне неудачными, и сейчас почти не употребляются.

В системе СГС:

U = E ⋅ D + B ⋅ H 8 π {\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} }{8\pi }}}

Энергия электромагнитного поля в колебательном контуре

Энергия электромагнитного поля в колебательном контуре:

W = C U 2 2 + L I 2 2 {\displaystyle W={\frac {CU^{2}}{2}}+{\frac {LI^{2}}{2}}}

U - электрическое напряжение в цепи, C - электроемкость конденсатора, I - сила тока, L - индуктивность катушки или витка с током.

Потоки энергии электромагнитного поля

Основная статья: Вектор Пойнтинга

Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в русской научной традиции - вектор Умова - Пойнтинга).

В системе СИ вектор Пойнтинга равен S = E × H {\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} } (векторному произведению напряжённостей электрического и магнитного полей) и направлен перпендикулярно векторам E и H. Это естественным образом согласуется со свойством поперечности электромагнитных волн.

Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей и имеет тот же вид: S = E × H {\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} } .

Факт существования потоков энергии в постоянных электрических и магнитных полях может выглядеть странно, но не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Энергию магнитного поля катушки индуктивности можно вычислить следующим способом. Для упрощения расчета рассмотрим такой случай, когда после отключения катушки от источника ток в цепи убывает со временем по линейному закону. В этом случае ЭДС самоиндукции имеет постоянное значение, равное

,

где t – промежуток времени, за который сила тока в цепи убывает от начального значения I до 0.

За время t при линейном убывании силы тока от I до 0 в цепи проходит электрический заряд:

,

поэтому работа электрического тока равна

Эта работа совершается за счет энергии магнитного поля катушки. Энергия магнитного поля катушки индуктивности равна половине произведения ее индуктивности на квадрат силы тока в ней:

1. Уравнение Максвелла. Электромагнитные волны.

Согласно теории Максвелла, переменное магнитное поле вызывает появление переменного вихревого эл. поля, которое, в свою очередь, вызывает появление переменного магнитного поля и т.д. Таким образом происходит распространение электромагнитных возмущений в пространстве т.е. распространяется электромагнитная волна. Основные свойства электромагнитных волн. 1. Электромагнитная волна – поперечная. 2. Скорость электромагнитных волн в вакууме равна v=c=3*108м/с и совпадает со скоростью света. В среде v=c/(), где  и  - диэлектрическая и магнитная проницаемости среды. 3. Электромагнитные волны переносят энергию. 4. Электромагнитные волны отражаются от проводящих поверхностей и преломляются на границе двух диэлектриков. 5. Электромагнитные волны оказывают давление на тела. 6. Если электромагнитная волна оказывает давление на тела, т.е. сообщает им импульс, следовательно, она также обладает импульсом. 7. Наблюдается дифракция, интерференция и поляризация электромагнитных волн.

М а ксвелла уравн е ния, фундаментальные уравнения классической макроскопической электродинамики , описывающие электромагнитные явления в произвольной среде. М. у. сформулированы Дж. К. Максвеллом в 60-х годах 19 века на основе обобщения эмпирических законов электрических и магнитных явлений. Опираясь на эти законы и развивая плодотворную идею М. Фарадея о том, что взаимодействия между электрически заряженными телами осуществляются посредством электромагнитного поля , Максвелл создал теорию электромагнитных процессов, математически выражаемую М. у. Современная форма М. у. дана немецким физиком Г. Герцем и английским физиком О. Хевисайдом .

М. у. связывают величины, характеризующие электромагнитное поле, с его источниками, то есть с распределением в пространстве электрических зарядов и токов. В пустоте электромагнитное поле характеризуется двумя векторными величинами, зависящими от пространственных координат и времени: напряжённостью электрического поля Е и магнитной индукцией В . Эти величины определяют силы, действующие со стороны поля на заряды и токи, распределение которых в пространстве задаётся плотностью заряда r (зарядом в единице объёма) и плотностью тока j (зарядом, переносимым в единицу времени через единичную площадку, перпендикулярную направлению движения зарядов). Для описания электромагнитных процессов в материальной среде (в веществе), кроме векторов Е и В , вводятся вспомогательные векторные величины, зависящие от состояния и свойств среды: электрическая индукция D и напряжённость магнитного поля Н .

М. у. позволяют определить основные характеристики поля (Е, В, D и Н ) в каждой точке пространства в любой момент времени, если известны источники поля j и r как функции координат и времени. М. у. могут быть записаны в интегральной или в дифференциальной форме (ниже они даны в абсолютной системе единиц Гаусса; см. СГС система единиц ).

М. у. в интегральной форме определяют по заданным зарядам и токам не сами векторы поля Е, В, D, Н в отдельных точках пространства, а некоторые интегральные величины, зависящие от распределения этих характеристик поля: циркуляцию векторов Е и Н вдоль произвольных замкнутых контуров и потоки векторов D и B через произвольные замкнутые поверхности.

Первое М. у. является обобщением на переменные поля эмпирического Ампера закона о возбуждении магнитного поля электрическими токами. Максвелл высказал гипотезу, что магнитное поле порождается не только токами, текущими в проводниках, но и переменными электрическими полями в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения. Ток смещения возбуждает магнитное поле по тому же закону, что и ток проводимости (позднее это было подтверждено экспериментально). Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым.

Первое М. у. имеет вид:

, (1, a)

то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S j n - проекция плотности тока проводимости j на нормаль к бесконечно малой площадкеds , являющейся частью поверхности S, - проекция плотности тока смещения на ту же нормаль, а с = 3×1010 см/сек - постоянная, равная скорости распространения электромагнитных взаимодействий в вакууме.

Второе М. у. является математической формулировкой закона электромагнитной индукции Фарадея (см. Индукция электромагнитная ) записывается в виде:

то есть циркуляция вектора напряжённости электрического поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S , ограниченную данным контуром. Здесь B n - проекция на нормаль к площадке ds вектора магнитной индукции В ; знак минус соответствует Ленца правилу для направления индукционного тока.

Третье М. у. выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):

то есть поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.

Четвёртое М. у. (обычно называемое Гаусса теоремой ) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов - Кулона закона :

, (1, г)

то есть поток вектора электрической индукции через произвольную замкнутую поверхность S определяется электрическим зарядом, находящимся внутри этой поверхности (в объёме V , ограниченном данной поверхностью).

Если считать, что векторы электромагнитного поля (Е, В, D, Н ) являются непрерывными функциями координат, то, рассматривая циркуляцию векторов Н и Е по бесконечно малым контурам и потоки векторов B и D через поверхности, ограничивающие бесконечно малые объёмы, можно от интегральных соотношений (1, а - г) перейти к системе дифференциальных уравнений, справедливых в каждой точке пространства, то есть получить дифференциальную форму М. у. (обычно более удобную для решения различных задач):

rot ,

Здесь rot и div - дифференциальные операторы ротор (см. Вихрь ) и дивергенция , действующие на векторы Н , Е , B и D . Физический смысл уравнений (2) тот же, что и уравнений (1).

М. у. в форме (1) или (2) не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Необходимо их дополнить соотношениями, связывающими векторы Е, Н, D, В и j , которые не являются независимыми. Связь между этими векторами определяется свойствами среды и её состоянием, причёмD и j выражаются через Е , а B - через Н :

D = D (E ), B = B (Н ), j = j (E ). (3)

Эти три уравнения называются уравнениями состояния, или материальными уравнениями; они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определённую форму. В вакууме D ºЕ и B º Н . Совокупность уравнений поля (2) и уравнений состояния (3) образуют полную систему уравнений.

Макроскопические М. у. описывают среду феноменологически, не рассматривая сложного механизма взаимодействия электромагнитного поля с заряженными частицами среды. М. у. могут быть получены из Лоренца - Максвелла уравнений для микроскопических полей и определённых представлений о строении вещества путём усреднения микрополей по малым пространственно-временным интервалам. Таким способом получаются как основные уравнения поля (2), так и конкретная форма уравнений состояния (3), причём вид уравнений поля не зависит от свойств среды.

Уравнения состояния в общем случае очень сложны, так как векторы D , B и j в данной точке пространства в данный момент времени могут зависеть от полей Е и Н во всех точках среды во все предшествующие моменты времени. В некоторых средах векторы D и B могут быть отличными от нуля при Е и H равных нулю (сегнетоэлектрики и ферромагнетики ). Однако для большинства изотропных сред, вплоть до весьма значительных полей, уравнения состояния имеют простую линейную форму:

D = eE , B = mH , j = sE + j cтр. (4)

Здесь e (x, у, z ) - диэлектрическая проницаемость , а m (x, у, z ) - магнитная проницаемость среды, характеризующие соответственно её электрические и магнитные свойства (в выбранной системе единиц для вакуума e = m = 1); величина s(x, у, z ) называется удельной электропроводностью; j cтр - плотность так называемых сторонних токов, то есть токов, поддерживаемых любыми силами, кроме сил электрического поля (например, магнитным полем, диффузией и т. д.). В феноменологической теории Максвелла макроскопические характеристики электромагнитных свойств среды e, m и s должны быть найдены экспериментально. В микроскопической теории Лоренца - Максвелла они могут быть рассчитаны.

Проницаемости e и m фактически определяют тот вклад в электромагнитное поле, который вносят так называемые связанные заряды, входящие в состав электрически нейтральных атомов и молекул вещества. Экспериментальное определение e, m, s позволяет рассчитывать электромагнитное поле в среде, не решая трудную вспомогательную задачу о распределении связанных зарядов и соответствующих им токов в веществе. Плотность заряда r и плотность токаj в М. у. - это плотности свободных зарядов и токов, причём вспомогательные векторы Н и D вводятся так, чтобы циркуляция вектора Н определялась только движением свободных зарядов, а поток вектора D - плотностью распределения этих зарядов в пространстве.

Если электромагнитное поле рассматривается в двух граничащих средах, то на поверхности их раздела векторы поля могут претерпевать разрывы (скачки); в этом случае уравнения (2) должны быть дополнены граничными условиями:

[nH ] 2 - [nH ] 1 = ,

[nE ] 2 - [nE ] 1 = 0, (5)

(nD ) 2 - (nD ) 1 = 4ps,

(nB ) 2 - (nB ) 1 = 0.

Здесь j пов и s - плотности поверхностных тока и заряда, квадратные и круглые скобки - соответственно векторное и скалярное произведения векторов, n - единичный вектор нормали к поверхности раздела в направлении от первой среды ко второй (1®2), а индексы относятся к разным сторонам границы раздела.

Основные уравнения для поля (2) линейны, уравнения же состояния (3) могут быть и нелинейными. Обычно нелинейные эффекты обнаруживаются в достаточно сильных полях. В линейных средах [удовлетворяющих соотношениям (4)] и, в частности, в вакууме М. у. линейны и, таким образом, оказывается справедливым суперпозиции принцип : при наложении полей они не оказывают влияния друг на друга.

Из М. у. вытекает ряд законов сохранения. В частности, из уравнений (1, а) и (1, г) можно получить соотношение (так называемое уравнение непрерывности):

представляющее собой закон сохранения электрического заряда: полный ток, протекающий за единицу времени через любую замкнутую поверхность S , равен изменению заряда внутри объёма V , ограниченного этой поверхностью. Если ток через поверхность отсутствует, то заряд в объёме остаётся неизменным.

Из М. у. следует, что электромагнитное поле обладает энергией и импульсом (количеством движения). Плотность энергии w (энергии единицы объёма поля) равна:

Электромагнитная энергия может перемещаться в пространстве. Плотность потока энергии определяется так называемым вектором Пойнтинга

Направление вектора Пойнтинга перпендикулярно как Е , так и Н и совпадает с направлением распространения электромагнитной энергии, а его величина равна энергии, переносимой в единицу времени через единицу поверхности, перпендикулярной к вектору П . Если не происходит превращений электромагнитной энергии в другие формы, то, согласно М. у., изменение энергии в некотором объёме за единицу времени равно потоку электромагнитной энергии через поверхность, ограничивающую этот объём. Если внутри объёма за счёт электромагнитной энергии выделяется тепло, то закон сохранения энергии записывается в форме:

где Q - количество теплоты, выделяемой в единицу времени.

Плотность импульса электромагнитного поля g (импульс единицы объёма поля) связана с плотностью потока энергии соотношением:

Существование импульса электромагнитного поля впервые было обнаружено экспериментально в опытах П. Н. Лебедева по измерению давления света (1899).

Как видно из (7), (8) и (10), электромагнитное поле всегда обладает энергией, а поток энергии и электромагнитный импульс отличны от нуля лишь в случае, когда одновременно существуют и электрическое и магнитное поля (причём эти поля не параллельны друг другу).

М. у. приводят к фундаментальному выводу о конечности скорости распространения электромагнитных взаимодействий (равной с = 3×1010 см/сек ). Это означает, что при изменении плотности заряда или тока в некоторой точке пространства порождаемое ими электромагнитное поле в точке наблюдения изменяется не в тот же момент времени, а спустя время t = R/c , где R - расстояние от элемента тока или заряда до точки наблюдения. Вследствие конечной скорости распространения электромагнитных взаимодействий возможно существование электромагнитных волн , частным случаем которых (как впервые показал Максвелл) являются световые волны.

Электромагнитные явления протекают одинаково во всех инерциальных системах отсчёта , то есть удовлетворяют принципу относительности. В соответствии с этим М. у. не меняют своей формы при переходе от одной инерциальной системы отсчёта к другой (релятивистски инвариантны). Выполнение принципа относительности для электромагнитных процессов оказалось несовместимым с классическими представлениями о пространстве и времени, потребовало пересмотра этих представлений и привело к созданию специальной теории относительности (А. Эйнштейн , 1905; см. Относительности теория ). Форма М. у. остаётся неизменной при переходе к новой инерциальной системе отсчёта, если пространств, координаты и время, векторы поля Е, Н, В, D , плотность тока j и плотность заряда r изменяются в соответствии с Лоренца преобразованиями (выражающими новые, релятивистские представления о пространстве и времени). Релятивистски-инвариантная форма М. у. подчёркивает тот факт, что электрическое и магнитное поля образуют единое целое.

М. у. описывают огромную область явлений. Они лежат в основе электротехники и радиотехники и играют важнейшую роль в развитии таких актуальных направлений современной физики, как физика плазмы и проблема управляемых термоядерных реакций , магнитная гидродинамика , нелинейная оптика , конструирование ускорителей заряженных частиц , астрофизика и т. д. М. у. неприменимы лишь при больших частотах электромагнитных волн, когда становятся существенными квантовые эффекты, то есть когда энергия отдельных квантов электромагнитного поля - фотонов - велика и в процессах участвует сравнительно небольшое число фотонов.

§ 130. Энергия магнитного поля

Проводник, по которому протекает элек­трический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезно­вением тока. Магнитное поле, подобно электрическому, является носителем энер­гии. Естественно предположить, что энер­гия магнитного поля равна работе, которая затрачивается током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому течет ток I . С данным контуром сцеплен магнитный поток (см. (126.1)) Ф=LI , причем при измене­нии тока на dI магнитный поток изменяет­ся на dФ=L dI . Однако для изменения магнитного потока на величину dФ (см. § 121) необходимо совершить работу dA =I dФ=LI dI. Тогда работа по созда­нию магнитного потока Ф будет равна

Следовательно, энергия магнитного поля, связанного с контуром,

W=LI 2 /2. (130.1)

Исследование свойств переменных маг­нитных полей, в частности распростране­ния электромагнитных волн, явилось до­казательством того, что энергия магнитно­го поля локализована в пространст­ве. Это соответствует представлениям те­ории поля.

Энергию магнитного поля можно пред-

ставить как функцию величин, характери­зующих это поле в окружающем простран­стве. Для этого рассмотрим частный слу­чай - однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получим

Так какI =В l / ( 0 N) (см. (119.2)) и В=  0  H (см. (109.3)), то

где Sl =V - объем соленоида.

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью

Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле (95.8) для объемной плотности энергии электроста­тического поля, с той разницей, что элек­трические величины заменены в нем маг­нитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднородных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В от Н линейная, т. е. оно относится только к пара- и диамагнетикам (см. § 132).

Контрольные вопросы

В чем заключается явление электромагнитной индукции? Проанализируйте опыты Фарадея.

Что является причиной возникновения э.д.с. индукции в замкнутом проводящем контуре? Отчего и как зависит э.д.с. индукции, возникающая в контуре?

Почему для обнаружения индукционного тока лучше использовать замкнутый проводник

в виде катушки, а не в виде одного витка провода?

Сформулируйте правило Ленца, проиллюстрировав его примерами.

Всегда ли при изменении потока магнитной индукции в проводящем контуре в нем возникает э.д.с. индукции? индукционный ток?

Возникает ли индукционный ток в проводящей рамке, поступательно движущейся в однород­ном магнитном поле?

Покажите, что закон Фарадея есть следствие закона сохранения энергии.

Какова природа э.д.с. электромагнитной индукции?

Выведите выражение для э.д.с. индукции в плоской рамке, равномерно вращающейся в одно­родном магнитном поле. За счет чего ее можно увеличить?

Что такое вихревые токи? Вредны они или полезны?

Почему сердечники трансформаторов не делают сплошными?

В чем заключаются явления самоиндукции и взаимной индукции? Вычислите э.д.с. индукции

для обоих случаев,

В чем заключается физический смысл времени релаксации =L/R Докажите, что оно имеет

размерность времени.

Приведите соотношение между токами в первичной и вторичной обмотках повышающего транс­форматора.

Когда э.д.с. самоиндукции больше - при замыкании или размыкании цепи постоянного тока?

Какая физическая величина выражается в генри? Дайте определение генри.

В чем заключается физический смысл индуктивности контура? взаимной индуктивности двух контуров? От чего они зависят?

Запишите и проанализируйте выражения для объемной плотности энергии электростатического и магнитного полей. Чему равна объемная плотность энергии электромагнитного поля?

Напряженность магнитного поля возросла в два раза. Как изменилась объемная плотность энергии магнитного поля?

Задачи

15.1. Кольцо из алюминиевого провода (=26 нОм м) помещено в магнитное поле перпендику­лярно линиям магнитной индукции. Диаметр кольца 20 см, диаметр провода 1 мм. Опреде­лить скорость изменения магнитного поля, если сила тока в кольце 0,5 А.

15.2. В однородном магнитном поле, индукция которого 0,5 Тл, равномерно с частотой 300 мин-1 вращается катушка, содержащая 200 витков, плотно прилегающих друг к другу. Площадь поперечного сечения катушки 100 см2. Ось вращения перпендикулярна оси катушки и направлению магнитного поля. Определить максимальную э.д.с., индуцируемую в катушке. .

15.3. Определить, сколько витков проволоки, вплотную прилегающих друг к другу, диаметром 0,3 мм с изоляцией ничтожной толщины надо намотать на картонный цилиндр диаметром 1 см, чтобы получить однослойную катушку с индуктивностью 1 мГн.

15.4. Определить, через сколько времени сила тока замыкания достигнет 0,98 предельного значе­ния, если источник тока замыкают на катушку сопротивлением 10 Ом и индуктивностью 0,4 Гн.

15.5. Два соленоида (индуктивность одного L 1 =0,36 Гн, второго L 2 = 0,64 Гн) одинаковой длины и практически равного сечения вставлены один в другой. Определить взаимную индуктив­ность соленоидов.

15.6. Автотрансформатор, понижающий напряжение с U 1 =5,5 кВ до U 2 =220 В, содержит в пер­вичной обмотке N 1 = 1500витков. Сопротивление вторичной обмотки R 2 =2 Ом. Сопротивле­ние внешней цепи (в сети пониженного напряжения) R =13 Ом. Пренебрегая сопротив­лением первичной обмотки, определить число витков во вторичной обмотке трансформатора.

37 Энергия магнитного поля

Проводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезнове­нием тока. Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затра­чивается током на создание этого поля.

Рассмотрим контур индуктивностью L , по которому течет ток I . С данным кон­туром сцеплен магнитный поток (см. (126.1)) Ф= LI , причем при изменении тока на dI магнитный поток изменяется на dФ=L dI . Однако для изменения магнитного потока на величину dФ (см. § 121) необходимо совершить работу dА= I dФ= LI dI . Тогда работа по созданию магнитного потока Ф будет равна

Следовательно, энергия магнитного поля, связанного с контуром,

(130.1)

Исследование свойств переменных магнитных полей, в частности распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля локализована в пространстве. Это соответствует представлениям теории поля.

Энергию магнитного поля можно представить как функцию величин, характеризу­ющих это поле в окружающем пространстве. Для этого рассмотрим частный слу­чай - однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получим

Так как I = Bl / ( 0  N ) (см. (119.2)) и В=  0  H (см. (109.3)), то

130.2)

где Sl = V - объем соленоида.

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью

(130.3)

Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле (95.8) для объемной плотности энергии электростатического поля, с той разницей, что электрические величины заменены в нем магнитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднород­ных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам (см. § 132).

38. Магнитные моменты электронов и атомов

Рассматривая действие магнитного поля на проводники с током и на движущиеся заряды, мы не интересовались процессами, происходящими в веществе. Свойства среды учитывались формально с помощью магнитной проницаемости  . Для того чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества.

Опыт показывает, что все вещества, помещенные в магнитное поле, намагничива­ются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в основу гипотезу Ампера (см. § 109), согласно которой в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах.

Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладаеторбитальным магнитным моментом (см. (109.2)) p m =IS n , модуль которого

(131.1)

где I = e  - сила тока,  - частота вращения электрона по орбите, S - площадь орбиты. Если электрон движется по часовой стрелке (рис. 187), то ток направлен против часовой стрелки и вектор р m (в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона, как указано на рисунке.

С другой стороны, движущийся по орбите электрон обладает механическим момен­том импульса L e , модуль которого, согласно (19.1),

(131.2)

где v = 2 ,  r 2 = S. Вектор L e (его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона .

Из рис. 187 следует, что направления р m и L e , противоположны, поэтому, учитывая выражения (131.1) и (131.2), получим

(131.3)

где величина

(131.4)

называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком «–», указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой ор­биты, хотя для разных орбит значения v и r различны. Формула (131.4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит.

Экспериментальное определение гиромагнитного отношения проведено в опытах Эйнштейна и де Гааза* (1915), которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном поле (по обмотке соленоида пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня). При исследовании вынужденных крутильных колебаний стержня определялось гиромагнитное отношение, которое ока­залось равным – (e / m ). Таким образом, знак носителей, обусловливающих молекуляр­ные токи, совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза большим, чем введенная ранее величина g (см. (131.4)). Для объяснения этого результата, имевшего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что кроме орбитальных моментов (см. (131.1) и (131.2)) электрон обладает собственным механическим моментом импульса L es , называ­емым спином . Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона L es , соответствует собственный (сотовый) магнитный момент р ms , пропорци­ональный L es и направленный в противоположную сторону:

(131.5)

*В. И. де Гааз (1878-1960) - нидерландский физик.

Величина g s называетсягиромагнитным отношением спиновых моментов.

Проекция собственного магнитного момента на направление вектора В может принимать только одно из следующих двух значений:

где ħ= h / (2)(h - постоянная Планка),  b -магнетон Бора, являющийся единицей магнитного момента электрона.

В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнитный момент атома, следовательно, складывается из магнитных моментов входящих в его состав электронов и магнитного момента ядра (обусловлен магнитными моментами входящих в ядро протонов и ней­тронов). Однако магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими пренебрегают. Таким образом, общий магнитный момент атома (молекулы) p a равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов:

(131.6)

Еще раз обратим внимание на то, что при рассмотрении магнитных моментов электронов и атомов мы пользовались классической теорией, не учитывая ограничений, накладываемых на движение электронов законами квантовой механики. Однако это не противоречит полученным результатам, так как для дальнейшего объяснения намаг­ничивания веществ существенно лишь то, что атомы обладают магнитными момен­тами.

Что такое Энергия магнитного поля катушки с током?

Almagul"

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА

Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл. цепь, обладает запасом энергии.
В момент замыкания эл. цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.

Энергия магнитного поля равна собственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.